Understanding the Balance: Exploring the Difference between Ratio and Proportion

In the vast landscape of mathematics, where numbers and relationships converge, ratio and proportion emerge as fundamental constructs that underpin a multitude of problem-solving scenarios. Often used interchangeably, these concepts, however, bear distinct characteristics, each playing a unique role in defining the balance and connections within mathematical frameworks. This blog post aims to unravel the intricacies of ratio and proportion, shedding light on their individual definitions, applications, and the nuanced differences that set them apart. 

As we delve into the realm of mathematics, we’ll unravel how ratios and proportions are articulated, examine practical examples, and explore the pros and cons of each. This journey, enriched by the guidance of maths tuition, aims to foster a thorough understanding of these essential mathematical tools.

What is Ratio and Proportion?

Ratio:

A ratio is a way of expressing the relationship between two quantities or numbers. It is essentially a comparison that highlights the relative size or magnitude of one quantity concerning another. Ratios can be represented in various forms, such as a fraction, with a colon, or using the word “to.” 

For instance, if there are three red apples and five green apples, the ratio of red apples to green apples can be expressed as 3:5 or 3/5.

Proportion:

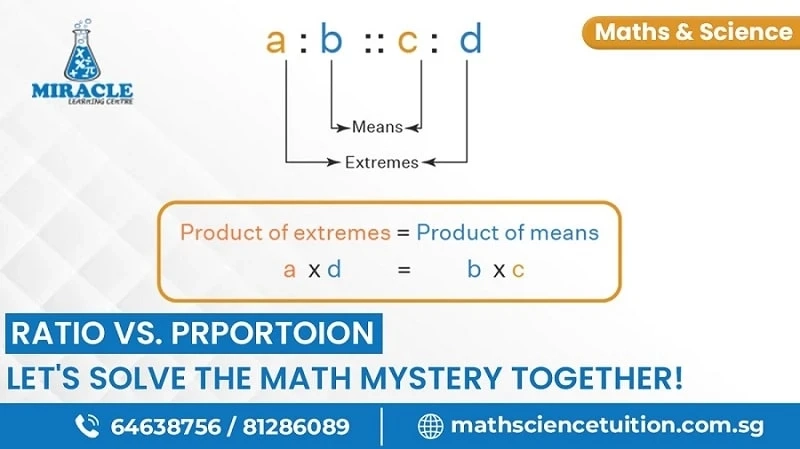
A proportion, on the other hand, is an equation that states that two ratios are equal. It involves setting up the comparison of two ratios to determine if they are in balance. In a proportion, the cross-products are equal, providing a basis for solving problems related to scaling, measurement, and comparison.

For instance, if you have a proportion involving the ratio of boys to girls as 2:3 and the ratio of girls to the total number of students as 3:8, you can set up the proportion:

2/3 = 3/8 or 2:3::3:8

This proportion can then be solved to find the missing quantity or determine if the given ratios are balanced.

Key Differences between Ratio and Proportion:

Ratio:

• Illuminates the quantitative dance between two or more quantities.
• Takes on various forms – a fraction, the elegant colon symbol (:), or the precise decimal form.
• Centers around the captivating act of comparing quantities.
• Offers no assurance of equal distribution, allowing for nuanced disparities.
• Intimately tied to comparison but without a commitment to even distribution.
• Example: Picture a schoolyard with a ratio of boys to girls standing proud at 3:2.
• Finds its way into real-life scenarios, waltzing through financial analyses and seasoning cooking recipes.
• Plays the field with an infinite array of possible values, a kaleidoscope of relational possibilities.
• Unraveling the art of ratios involves the magic of simplification or the grandeur of expansion, a transformative process.
• Puts emphasis on the sequence of terms – the order matters; 2:1 is a different story from 1:2.

Proportion:

• Sings the song of equality between two ratios.
• Stands tall with the symbolic “=” sign, a visual anthem of equilibrium.
• Delves into the harmonious relationship between parts and the whole.
• Requires the theatrical comparison of two ratios, a quest for equilibrium.
• Stands as the sentinel of balance, ensuring a symmetrical distribution.
• Example: Envision a class of 50 students, where the ratio of boys to girls maintains a harmonious 3:2.
• Takes center stage in solving proportion word problems and gracefully scaling measurements.
• Proudly boasts of having a singular solution, a mathematical maestro with a focused repertoire.
• Invokes the grandeur of cross-multiplication or the balletic unitary method in solving its puzzles.
• Throws convention to the wind – in proportions, the order of terms is a mere footnote; 2:1 is a poetic reflection of 1:2.

Advantage and Disadvantage:

Advantage of Ratio:

• Efficient Comparison: Simplifies diverse quantity comparisons.
• Accurate Scaling: Ensures precise proportionate adjustments.
• Financial Insight: Crucial for assessing company profitability and solvency.
• Problem-Solving Tool: Valuable for effective math problem-solving
• Consistent Evaluation: Enables consistent performance assessment.
• Visual Representation: Enhances understanding through visual representation.

Disadvantage of Ratio:

• Risk of Misinterpretation: Inadequate context may lead to flawed analysis.
• Subjectivity: Ratio interpretation involves subjective judgment, introducing bias.
• Limited Scope: Ratios oversimplify complex situations, focusing on quantity relationships.
• Data Dependency: Ratios rely heavily on accurate and available data, posing challenges.
• Inconsistent Units: Comparing ratios with different units can be misleading.
• Overemphasis on Numbers: Relying solely on ratios may overlook qualitative aspects.

Advantage of Proportion:

• Precision in Scaling: Proportions ensure accurate scaling for precise representations and adjustments.
• Unknowns Resolution: Proficient in solving unknown values through cross-multiplication or the unitary method.
• Estimation and Prediction: Establishes links between known quantities and unknowns, aiding in estimation and prediction.
• Geometry and Similarity: Crucial in geometry for determining shape similarity and calculating corresponding side lengths.
• Percentage Precision: Fundamental for percentage calculations, allowing for conversions, discounts, and precise mark-up calculations.
• Enhanced Reasoning: Proficiency in proportions fosters logical thinking and effective problem-solving through proportional reasoning skills.

Disadvantage of Proportion:

• Complex Problem Solving: Proportions present challenges in intricate problem-solving, demanding a solid grasp of underlying concepts.
• Misapplication Risk: Incorrect use or misinterpretation can yield erroneous results and flawed analysis.
• Limited Applicability: Not universally relevant, some relationships resist expression through ratios.
• Dependency on Equalities: Heavily reliant on equal ratios; any deviation undermines the proportional relationship.
• Assumptions and Simplifications: Proportions often involve simplifications, potentially missing real-world complexities.
• Nonlinear Relationships: Assuming linearity, proportions may inaccurately represent nonlinear phenomena.

How Maths Tuition in Singapore Enhances Understanding

Embarking on a journey to comprehend the nuances of ratio and proportion can be challenging, but Maths Tuition in Singapore offers a tailored approach to facilitate a deeper understanding. With skilled Maths Tutors leading the way, these programs provide a structured and supportive environment that goes beyond traditional classroom settings.

Maths Tuition, particularly in Singapore, is designed to break down complex mathematical concepts, making them more accessible to learners. Experienced Maths Tutors guide students through practical examples, offering personalized attention to address individual learning styles and challenges. This focused approach fosters a more profound grasp of ratios and proportions.

Engaging in Maths Tuition goes beyond the standard classroom experience, offering students the opportunity to ask questions freely, receive constructive feedback, and practice problem-solving techniques. The tailored guidance provided by Maths Tutors creates a conducive learning atmosphere, ensuring that students not only understand the principles of ratio and proportion but also gain confidence in applying them to real-world scenarios.

Conclusion:

In conclusion, mastering the intricacies of ratio and proportion is pivotal for anyone delving into the realms of mathematics. These fundamental tools unlock a world of problem-solving possibilities. Whether you’re a student striving for excellence or an enthusiast exploring the beauty of numbers, enrolling in maths tuition becomes a strategic investment. Experienced tutors can provide personalized guidance, ensuring that you confidently navigate the complexities of ratio and proportion, propelling you toward mathematical proficiency.