Geometry, the study of shapes, sizes, and properties of space, unveils a world filled with intricate relationships and patterns. One fascinating aspect of geometry is the exploration of angles, which play a fundamental role in defining shapes and their characteristics. In the realm of angles, the concept of "pairs of angles" emerges as a captivating subject that offers insights into geometric configurations and mathematical principles. Understanding pairs of angles becomes essential as students continue on their mathematical journey, and institutes such as Miracle Learning Centre provide excellent Maths tuition to elucidate this intriguing domain. In this exploration, we delve into the world of pairs of angles, unravelling their types, properties, and significance in both mathematics and the real world.
Understanding Angles:
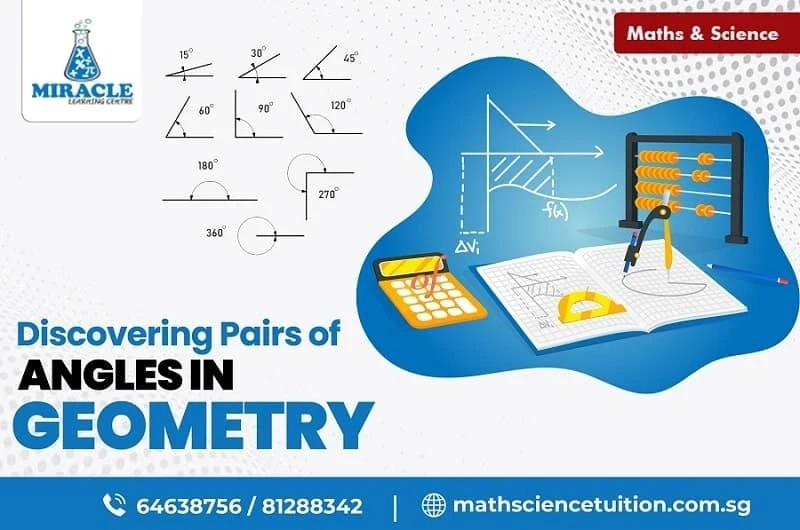
Before delving into pairs of angles, it is crucial to grasp the basics of angles. An angle is formed by two rays that share a common endpoint, known as the vertex. The rays are often referred to as the arms of the angle. The measurement of an angle is typically given in degrees, with a full circle encompassing 360 degrees. Angles can be categorized based on their measurements:
- Acute Angle: An angle measuring less than 90 degrees.
- Right Angle: An angle measuring exactly 90 degrees.
- Obtuse Angle: An angle measuring more than 90 degrees but less than 180 degrees.
- Straight Angle: An angle measuring exactly 180 degrees.
- Reflex Angle: An angle measuring more than 180 degrees but less than 360 degrees.
- Full Angle: An angle measuring exactly 360 degrees.
Exploring Pairs of Angles:
Pairs of angles are formed when two intersecting lines or line segments create angles at the intersection point. These pairs of angles exhibit distinct relationships and properties that provide valuable insights into geometry and mathematical principles. Some notable pairs of angles include:
Vertical Angles:
Vertical angles are formed when two intersecting lines create opposite angles that share a common vertex. These angles have equal measures, regardless of the angles\' size. Visualize an "X" shape formed by two intersecting lines: the angles at the ends of each "arm" are vertical angles.
For instance, if angle A measures 50 degrees, its vertical angle B will also measure 50 degrees. In everyday scenarios, consider an open pair of scissors – the angles between the blades are vertical angles. This fundamental concept of equality between vertical angles underlines the symmetrical nature of intersecting lines.
Adjacent Angles:
Adjacent angles are a fundamental concept in geometry, showcasing the proximity and interaction of angles. Formed by intersecting lines, adjacent angles share a common vertex and side while maintaining separate interiors. Picture an open book – the pages form adjacent angles at the binding.
In this scenario, if one angle measures 40 degrees, its adjacent angle might measure 140 degrees to complete the straight angle of 180 degrees.
The concept of adjacent angles finds practical use when folding paper, creating corners, and understanding the layout of objects. It\'s a simple yet essential concept that illustrates how angles coexist and influence our visual world.
Complementary Angles:
Complementary angles are a fascinating pair of angles that hold a special relationship in geometry. When two angles are complementary, their measures sum up to precisely 90 degrees. This unique property frequently arises in real-world scenarios. Imagine a right-angled triangle: one angle is 90 degrees, making it a right angle. The other two angles are complementary, meaning their combined measurements complete the right angle.
For instance, if one angle measures 30 degrees, the other angle must measure 60 degrees to satisfy the complementary property. Complementary angles find practical use in fields like carpentry, where ensuring precise right angles is crucial for constructing stable structures.
Supplementary Angles:
Supplementary angles are a pair of angles that, when combined, sum up to 180 degrees. In simpler terms, they form a straight line when placed side by side. A classic example can be observed with a door that opens and closes. As the door swings, the angles formed by the door and the door frame are supplementary.
If one angle measures 120 degrees, the other will measure 60 degrees, always adding up to a total of 180 degrees. This concept finds practical application in fields like navigation, where bearings are measured from a reference direction and often involve supplementary angle calculations.
Alternate Interior Angles:
Alternate interior angles are a crucial concept in geometry, particularly when dealing with parallel lines and a transversal. When a transversal crosses two parallel lines, alternate interior angles are formed on the inside of the parallel lines and on opposite sides of the transversal. These angles are equal in measure and play a vital role in proving theorems about parallel lines.
For instance, consider two parallel lines cut by a transversal. If angle A and angle B are alternate interior angles, then their measures are equal: ∠A = ∠B. This relationship is foundational in establishing the equality of angles in various geometric scenarios involving parallel lines.
Alternate Exterior Angles:
Similar to alternate interior angles, These angles are also congruent and contribute to the understanding of parallel lines. Situated on the exterior of the parallel lines and on opposite sides of the transversal, alternate exterior angles exhibit a unique balance. Notably, alternate exterior angles are congruent, signifying that they possess equal measures.
For instance, consider two parallel lines intersected by a transversal. If Angle A1 and Angle A2 are alternate exterior angles, their measures will be equal. This property plays a pivotal role in proving theorems related to parallel lines, shedding light on the intricate symmetries within geometry.
Corresponding Angles:
In the realm of geometry, corresponding angles emerge as key players when parallel lines intersected by a transversal come into play. Positioned in matching locations on either side of the transversal, corresponding angles hold equal measures. Imagine two parallel train tracks intersected by a road (the transversal).
As you gaze from above, the angles formed at each intersection are corresponding angles. These angles not only assist in proving the parallelism of lines but also lay the foundation for trigonometry and various real-world applications, showcasing the intriguing connections between seemingly disparate mathematical concepts and tangible scenarios.
Amidst the diverse applications of pairs of angles, their significance in education cannot be overlooked. For students seeking to grasp the complexities of geometry and angle relationships, quality maths tuition becomes a guiding light. In Singapore, a hub of educational excellence, the Miracle Learning Centre stands out as a premier destination for comprehensive maths tuition.
As a leading maths tuition centre in Singapore, Miracle Learning Centre employs innovative teaching methods to demystify concepts like pairs of angles, nurturing students\' understanding and enthusiasm for geometry. Through institutions like these, students embark on a journey that extends beyond angles, instilling a lifelong love for learning and mathematical exploration.
Conclusion
Pairs of angles provide a rich landscape for exploration within the realm of geometry and mathematics. From vertical angles to corresponding angles, these geometric relationships unveil a tapestry of interconnectedness that extends beyond theoretical knowledge. In Singapore, where a strong foundation in mathematics is highly valued, concepts like these fuel the mission of institutions like Miracle Learning Centre, a prominent maths tuition centre. Through its commitment to nurturing mathematical aptitude, this renowned centre contributes to shaping the future of aspiring learners. In the vibrant tapestry of angles, the intersection of mathematical exploration and practical application finds its harmony at the heart of maths tuition.